Visualization
Examine the visualization of consistencies across prediction tasks.
Visualization Page

Cross-Task Consistent Learning. The lower and upper rows show the results of the baseline (independent learning) and learning with cross-task consistency. The latter yields higher quality (especially at hard-to-predict fine-grained details) and more consistent predictions. Red boxes provide magnifications.
3) How can we design a learning system that makes consistent predictions?
This paper proposes a method which, given an arbitrary dictionary of tasks, augments the learning objective with explicit constraints for cross-task consistency. The constraints are learned from data rather than apriori given relationships. For instance, it is not necessary to encode that surface normals are the 3D derivative of depth or occlusion edges are discontinuities in depth. This makes the method applicable to any pairs of tasks as long as they are not statistically independent; even if their analytical relationship is unknown, hard to program, or non-differentiable.
The primary concept behind the method is

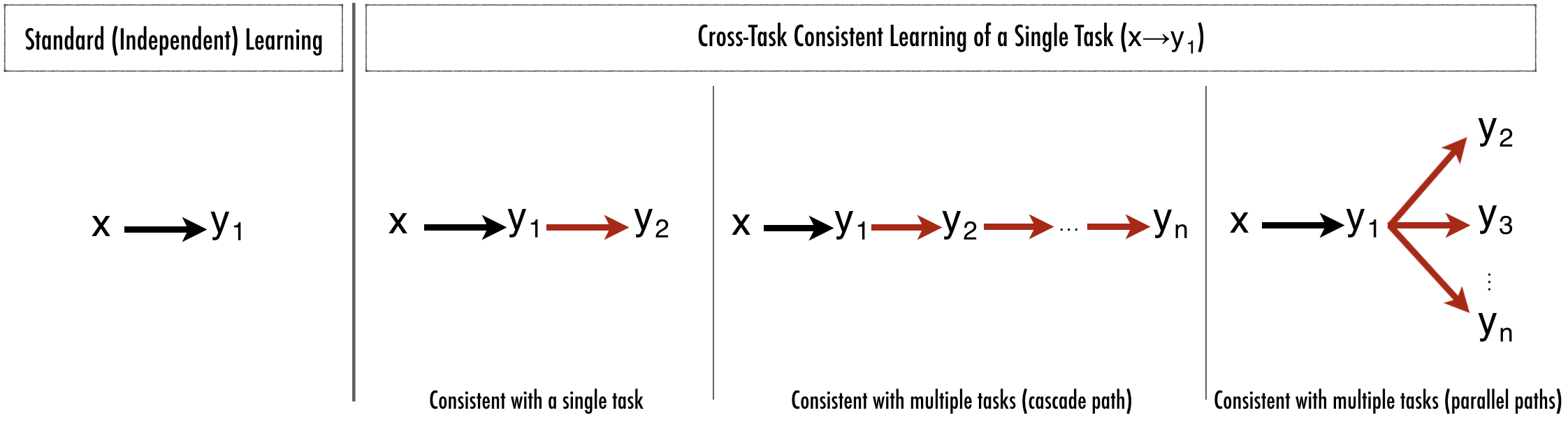
Enforcing cross-task consistency. (a) shows the typical multitask setup where predictors x→y1 and x→y2 are trained without a notation of consistency (either completely independently or with a shared encoder and dedicated decoders). (b) depicts the elementary triangle consistency constraint where the prediction x→y1 is enforced to be consistent with x→y2 using a function that relates y1 to y2 (i.e. y1→y2). (c) shows how the triangle unit from (b) can be an element of a larger system of domains. Finally, (d) illustrates the generalized case where in the larger system of domains, consistency can be enforced using invariance along arbitrary paths, as long as their endpoints are the same (here the blue and green paths). This is the general concept behind "inference-path invariance". The triangle in (b) is the smallest unit of such paths.
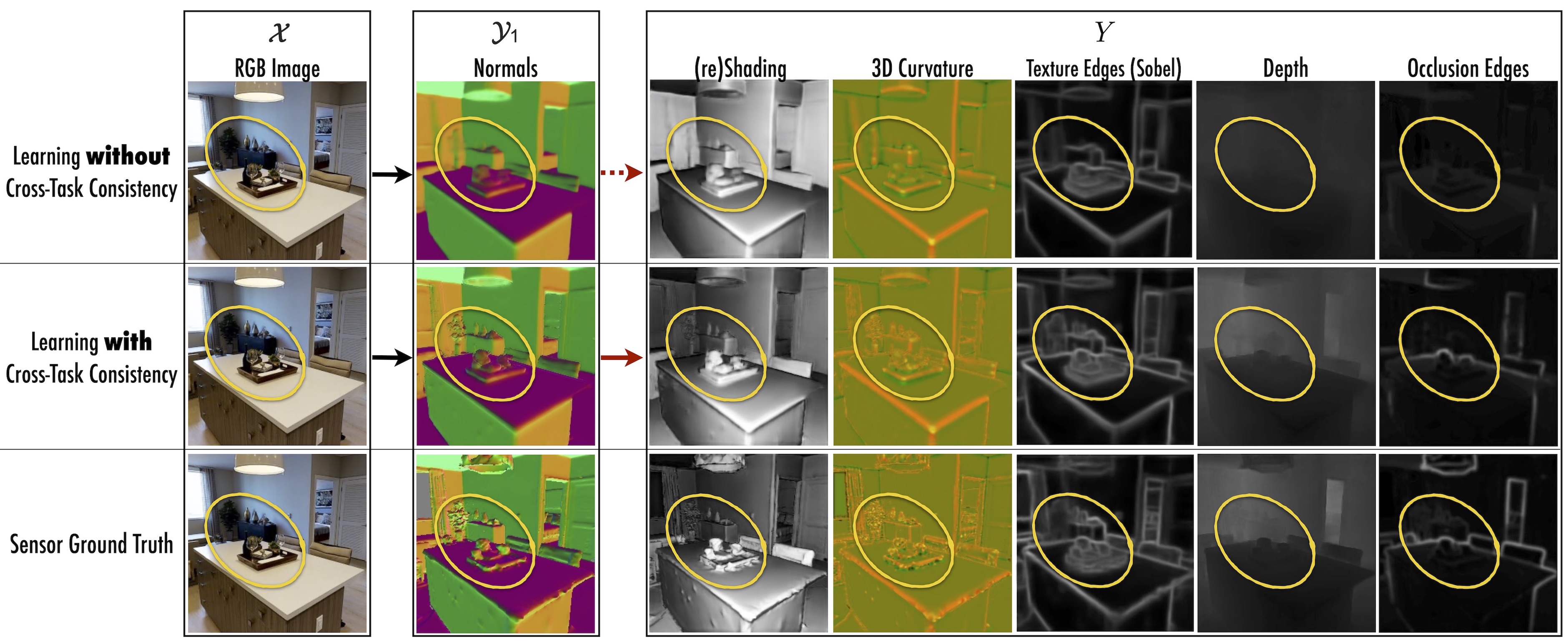
Learning with and without cross-task consistency shown for a sample query. Using the notation x→y1→Y, here x is RGB image, y1 is surface normals, and five domains in Y are reshading, 3D curvature, texture edges (Sobel filter), depth, and occlusion edges. Top row shows the results of standard training of x→y1. After convergence of training, the predicted normals (y1) are projected onto other domains (Y) which reveal various inaccuracies. This demonstrates such cross-task projections y1→Y can provide additional cues to training x→y1. Middle row shows the results of consistent training of x→y1 by leveraging y1→Y in the loss. The predicted normals are notably improved, especially in hard to predict fine-grained details (zoom into the yellow markers). Bottom row provides the ground truth.
This video demonstrates the same results as the above figure, but over a video and for depth prediction. The video is processed frame-by-frame.
Let's say that you're interested in predicting some y1 given x (For example surface normals given an RGB image). Instead of simply training a network to do x→y1 (i.e. RGB→Surface Normals), train it to do x→y1→y2 (i.e. RGB→Surface Normals→y2). It will fit the data better with improved RGB→Surface Normal predictions.
Many options for y2 work; even if you have only (x,y1) training data. All choices gave some benefit, though some more than others. Some y2 options:
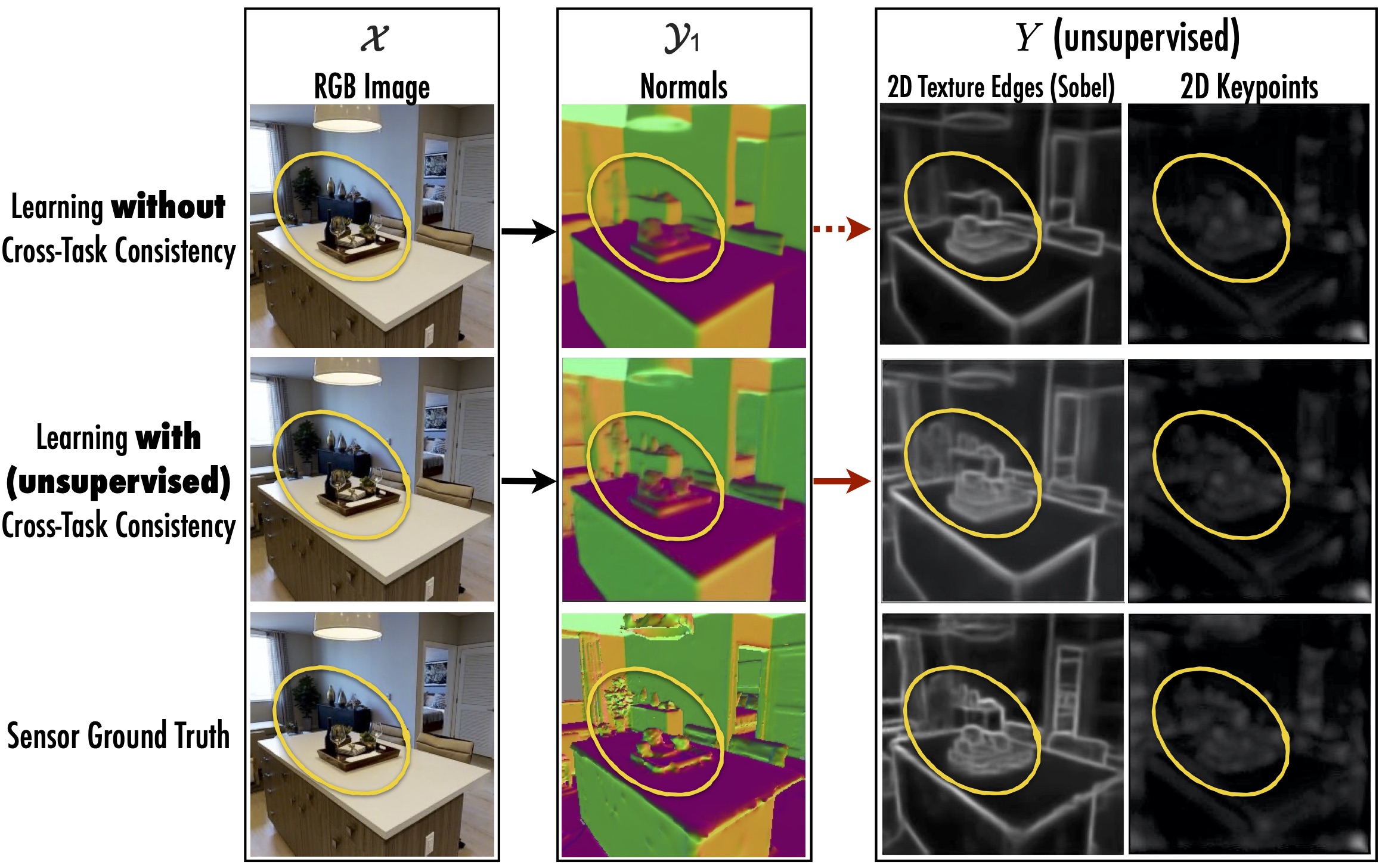
Results from using unsupervised consistency constraints. The network trained with cross-task consistency used only 2D edges and 2D keypoints as 'y2' tasks. Since these are unsupervised tasks, they required no additional supervision. Still, the consistency-trained network better fits the fine-grained details in images, as shown in the area highlighted with yellow circles. This echoes cross-task constraints are useful for common single-task learning too, even when no additional tasks/data/labels are available.
Below you can see sample results of learning with cross-task consistency for three sample prediction domains (surface normals, depth, (re)shading) over video and image queries. The video results are on external YouTube videos and the predictions are made frame-by-frame with no temporal smoothing. Zoom in to see the fine-grained details.

Cross-Task Consistent learning results on external domain data. Queries: Bedroom in Arles, Van Gogh (1888); Cotton Mill Girl, Lewis Hine (1908); Chernobyl Pripyat Abandoned School (c. 2009). Try the models on your own images at the live demo page.
Comparison with baselines: Below are some representative results from using cross-task consistent learning and various baselines. You can run comparisons yourself by uploading images on our live demo
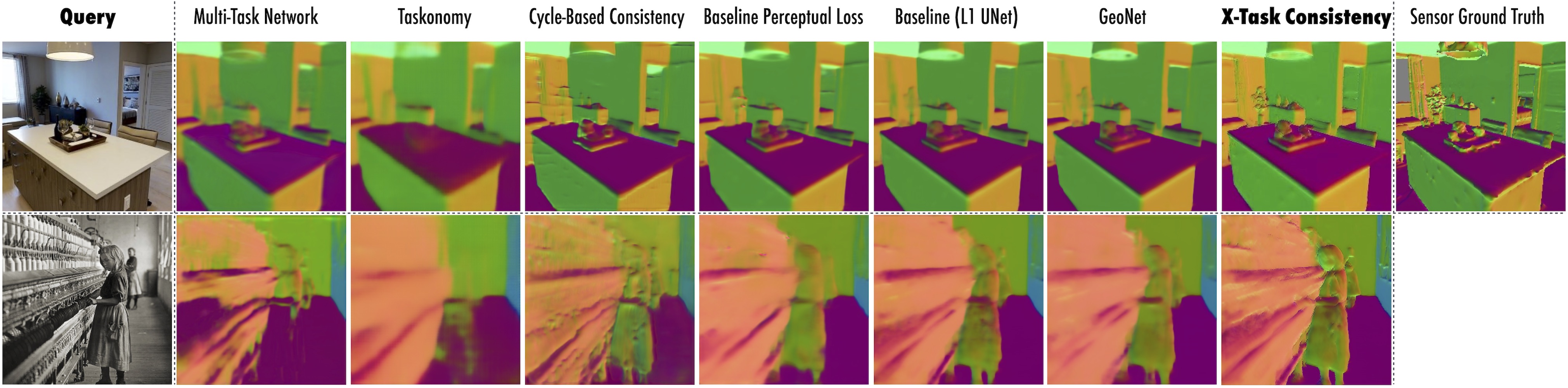
Networks trained with cross-task consistency, or with alternative baselines. The queries are from Taskonomy dataset (top) or external data (Cotton Mill Girl, Lewis Hine 1908; bottom).
The video shows a similar comparison where predictions are made frame-by-frame.
We quantify the amount of inconsistency in a prediction made for a query using an energy-based quantity called Consistency Energy. It is defined to be the standardized average of pairwise inconsistencies. This is also equivalent to the sample variance of the predictions. The consistency energy is an intrinsic quantity of the system, as it requires no ground truth and can be computed without any supervision. As shown below, the energy strongly correlates with supervised error and distributions shifts. This suggests the energy can be adopted as an unsuervised confidence metric.
Empirical analyses of consistency energy.
The video shows the energy vs two continuous domain shifts (JPEG compression, Blur). The domain shift distortions are applied on the frames. The energy turns out to be an unsupervised indicator of domain shift and generally correlates with the magnitude of shift.
To convey a more tangible understanding of learning with cross-task consistency constraints versus baselines, we compare the results of various configurations frame-by-frame on a youtube video. Visit the visualizations page to specify the comparison configuration of your choice and compare the performance.
Input Image

3D Ken Burns*
Input Image

3D Ken Burns*
Input Image

3D Ken Burns*
*Using the depth predicted by the consistency-based models and Niklaus et al. 2019 Ken Burn codeusing depth predicted by the consistency-based model








